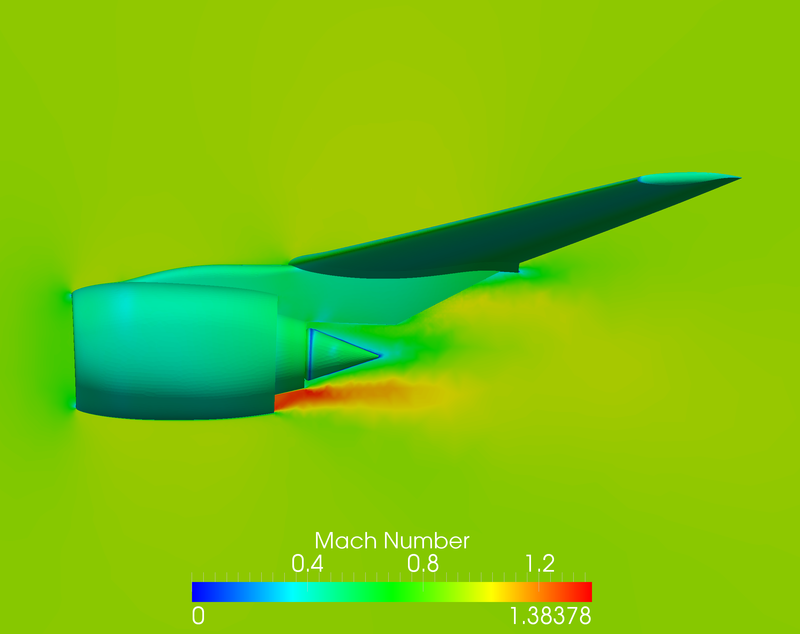
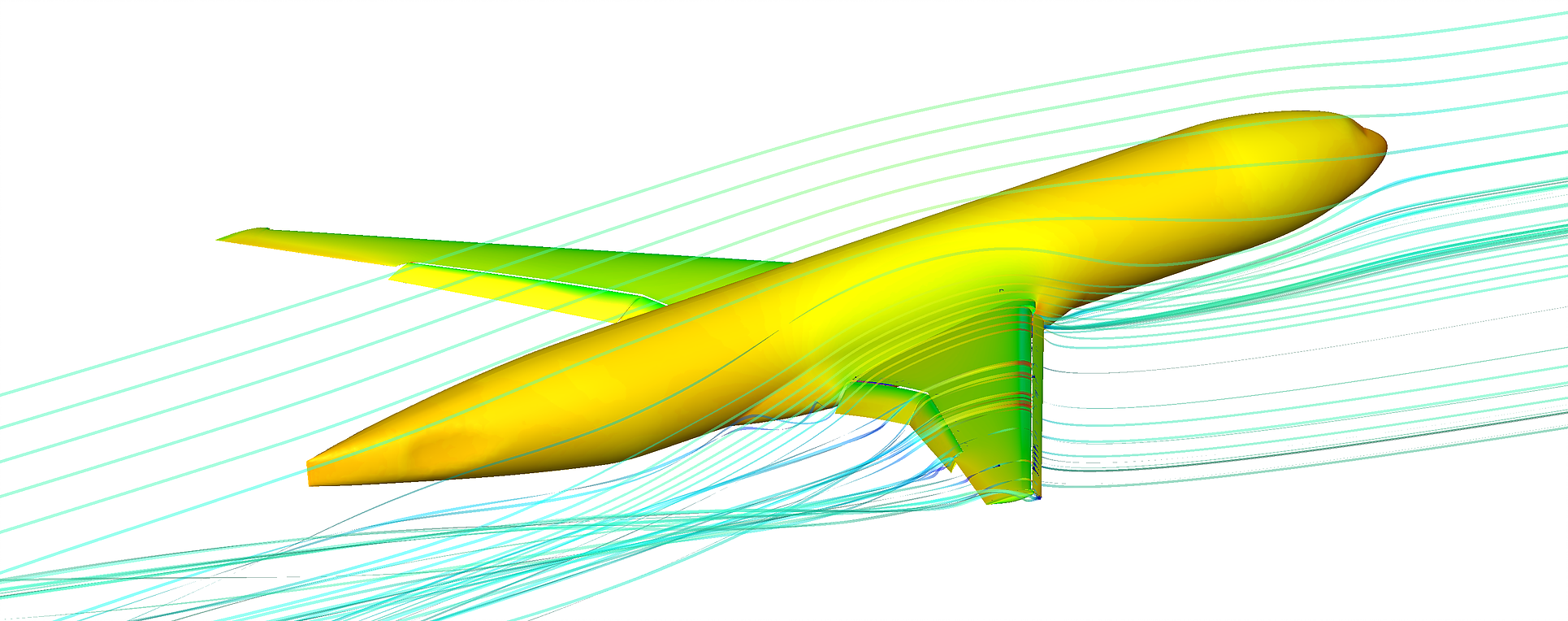
HOMA(High-Order Multilevel Adaptive) solver is a continuous finite-element framework
for the solution of RANS equations on unstructured grids. High-order discretizations,
scalable preconditioning techniques, and multigrid capabilities are important features
of this flow solver.
For parallelization, it uses MPI. In this solver, the time
integration is fully implicit, and automatic differentiation is used for the exact linearization.
For non-linear advancements, two principle algorithms are used: (1) a Newton-Krylov method
based on the Pseudo-Transient Continuation (PTC), and (2) a spectral multigrid algorithm based
on the full approximation scheme (FAS). For preconditioning of the linear systems, implicit line
relaxation, incomplete factorization, and additive Schwarz method (ASM) have been built into the code.
Also, the PETSc library has been integrated into the code, through which, external packages such as
BoomerAMG and Trilinios are accessible for algebraic multigrid (AMG) preconditioning.