Optimization: Adjoint Method
Adjoint methods are now well established as the most efficient technique for obtaining the
required design sensitivities, since these methods allow the computation of the sensitivities
of an arbitrary number of design parameters with respect to an objective or constraint at the
cost of the solution of a single adjoint problem, which is generally equivalent to the cost
of a flow analysis solution.
Our group has applied the adjoint methods to a variety of optimization problems. These include
aerodynamics, aero-acoustics, and structural dynamics. To create a more realistic and useful optimization tool
these disciplines have been combined to perform tightly coupled multidisciplianry adjoint problems.
This method has even been applied not only to steady state flow problems but also unsteady flow problems
like rotorcraft applications.
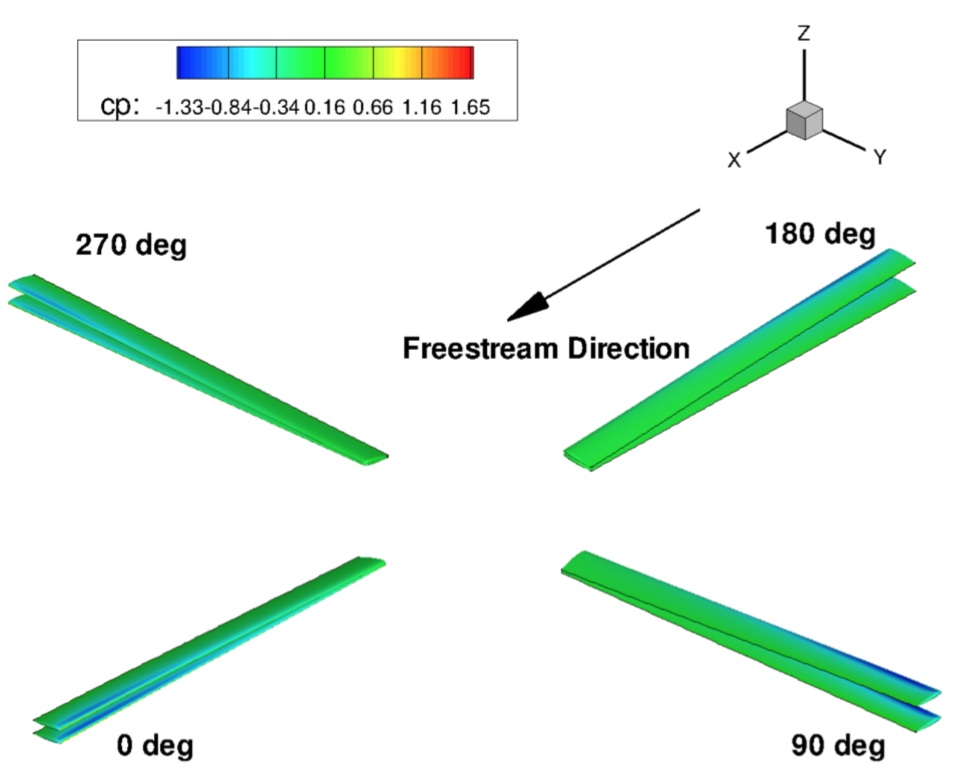
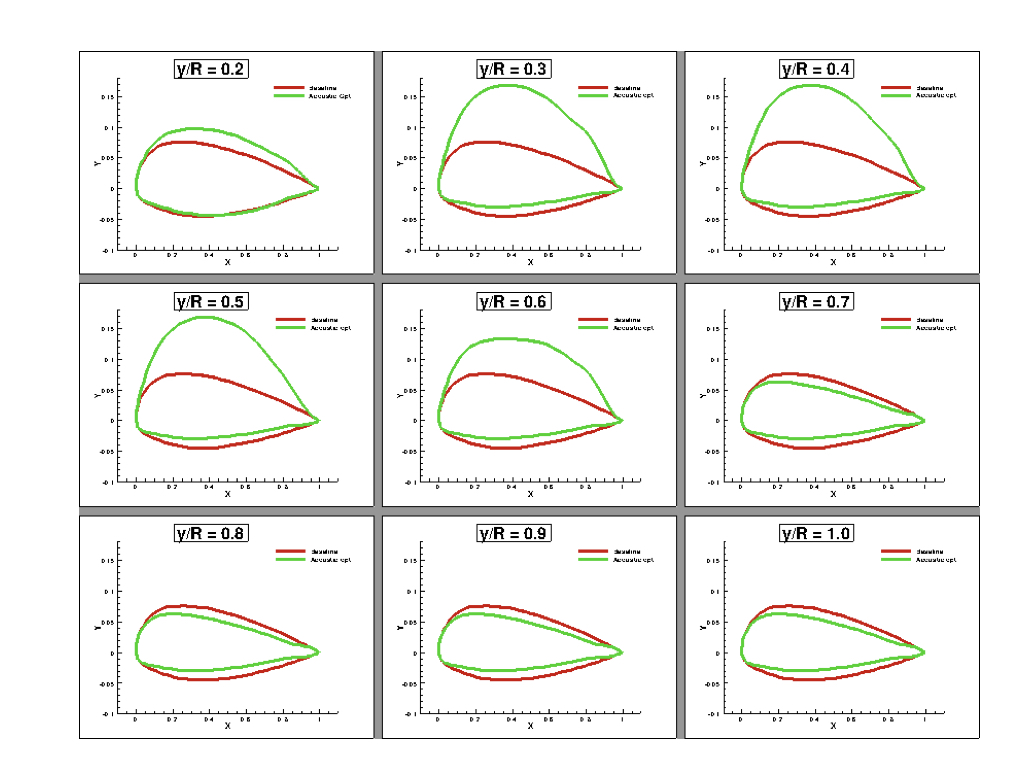
Aero-structural & acoustic Optimization
Since the blade flexibility affects the noise signature there is a
need for coupled aero-acoustic optimization for flexible blades.
- Enable blade shape (and other) optimization to minimize far-field acoustic signature
- Develop coupled near-field/far-field acoustic analysis and sensitivity capability for flexible rotors
- Use to perform time-dependent optimization for far-field acoustic objectives
- Demonstrate multidisciplinary capability (Combine aeroelastic and aeroacoustic adjoint)
Hart-II Rotor in Forward Flight
- Initial trim formulated as separate optimization problem
- Aeroacoustic optimization
- Torque optimization with acoustic constraint
- SNOPT constrained optimizer (Enforces constraints directly
Requires adjoint calculation for each objective/constraint)
